こんにちは。管理人のMです。
今回は『三平方の定理』について説明していきます。
『三平方の定理』は別名『ピタゴラスの定理』とも言います。
カタカナにするだけで少しレベルが上がって難しい感じがするのは自分だけでしょうか?
でも大丈夫!!公式を一つ覚えるだけで全問解けますよ。
この記事のターゲットです。
・学校で三平方の定理を習い始めた人
・三平方の定理の予習をしたい人
・テスト前に基本だけ押さえたい人
三平方の定理とは





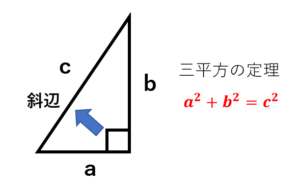
三角形の角の反対側にある辺を対辺と言います。
そして特に直角の対辺を斜辺を言います。
また、当然ですが、三角なので辺は3つあります。
三平方の定理とは、『斜辺の2乗が、その他の辺の2乗の和に等しくなる』というものです。
それは直角の位置を常に固定するクセをつけるということです。





<例題1>次のxとyを求めよ。

解答は最後にまとめています。
三平方の定理の逆




<例題2>次のうち直角三角形であるものはどれか。
(1) 3辺の長さがそれぞれ4cm,6cm,9cmの三角形
(2) 3辺の長さがそれぞれ6cm,8cm,10cmの三角形
(3) 3辺の長さがそれぞれ3cm,3cm,3√3cmの三角形
解答は最後にまとめています。
有名な直角三角形(覚えておくと便利!)

ところで、できることなら楽に解きたくないですか?







大変だと思いますが、覚えておくと問題を解くのが楽になります。
もちろん覚えなくても問題は解けます。
しかし覚えておくだけで「計算ミスを減らす」「回答時間を短縮する」「直角三角形を瞬時に見つける」ということでいいことづくめです。
普段は積極的に覚えようとすることを推奨しませんが、ここだけは頑張って覚えてもらいたい部分です。
<例題3>次のxとyを求めよ。

解答は最後にまとめています。
三平方の定理の証明




<証明>
まず、直角三角形を用意します。

次に、この三角形を4つ下の図のように並べます。

一辺がa+bの正方形と一辺がcの正方形と最初に用意した三角形が見えますね。
ここで、各図形の面積を考えると次のような関係であることが言えます。

この関係を数式で表して計算していきます。

以上で三平方の定理が導けました。



例題の解答・解説
<例題1>

公式に当てはめて計算していくのですが、最後にポイントが一つあります。
求めたい値は三角形の辺の長さなので、必ず正の値です。
平方根を求めるときに注意してください。
<例題2>

三平方の定理に代入して式が成立するかを考えましょう。
ポイントは最も大きい値を斜辺の部分に代入することです。
<例題3>


有名な直角三角形の辺の比を覚えておけば、三平方の定理に代入して解くよりも早く簡単に解けますね。
まとめ
いかがでしたでしょうか。
まずは、三平方の定理を使った計算ができること。そして、次は有名な直角三角形の辺の比を覚えておくこと。
この二つができれば三平方の定理の計算は全問解けます。
実は三平方の定理は単に計算問題だけでなく、平面図形や空間図形で答えを導くための道具として使う場面も多いです。
それはまたの機会に説明しますので、まずは演習編でガンガン問題演習してください。
お疲れさまでした。^^