こんにちは。管理人のMです。
今回は中学数学の確率~クジ引き~について説明していきます。
確率~コイン~を読んでいない方は、そちらから読むことをオススメします。
【中学数学】確率~コイン~【授業編】
クジ引きも身近な確率です。
祭りの宝クジとかやったことあるんじゃないですか?
最近の子はヒ〇ルさんの影響でやらない人も多いんですかね?
僕が小中学生の頃は景品の遊戯王のパック欲しさにお小遣いを全部吸われてましたが、今となってはいい思い出です。
ところで、確率の問題によく『同様に確からしい』という言葉が書かれていると思います。
あれはコインなら表も裏もほぼ同じ確率で出るし、サイコロならどの目もほぼ同じ確率で出るということを言っています。
要はインチキしていないってことです。



この記事のターゲットです。
・学校で確率を習い始めた人
・確率の予習をしたい人
・テスト前に基本だけ押さえたい人
・宝くじを当てて富豪になりたい人
確率の考え方(復習)
確率の考え方を復習しておきましょう。
確率とは、すべての起こりうるパターンのうちで特定のパターンがいくつあるかを考えるんでしたね。
【確率の考え方】
ある特定の出来事Aが起こる確率pは、次の式で求められる。
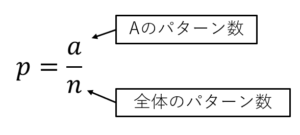
このときAの起こらない確率はqは、次の式で求められる。
![]()
クジ引き
ここからが本題です。


アタリが2本、ハズレが2本入っているクジを例に考えてみましょう。

赤がアタリで青がハズレです。
例題1
このクジを1回引くときに、アタリを引く確率を求めよ。




例題2
このクジを2個同時に引くときに、2つともアタリを引く確率を求めよ。





ちなみに今回は同時に引きましたが、同時に2個引こうが、1度引いた後にクジを戻さずもう1度引いた場合も確率は同じです。
同時に引こうが順番に引こうが最終的に手元に来るクジは変わらないので当たりまえですね。
ただし、順番に引くときに1度引いたクジを戻すと確率は変わってきます。
それを次の例題で見ていきましょう。
例題3
このクジを1回引き、結果を確認した後に引いたクジを戻してもう1度引いたときに2回ともアタリの確率を求めよ。


樹形図を作ってみます。
今回は1回引いたクジを戻すので、2回連続で同じクジを引くことがあることに注意しましょう。
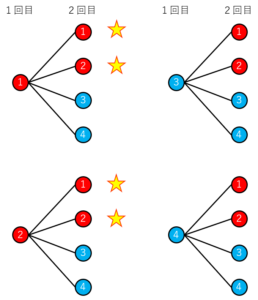
クジの引き方は16通りあることが分かります。
その中で2回ともアタリを引いているのは4通りなので、
求める確率は16分の4、約分して4分の1となります。

まとめ
クジ引きの確率、いかがでしたか?
4個中アタリが2個のクジはとても良心的ですよね。
本物のクジは数百個の中にアタリが0個1個なんてこともあるので、いかに当てるのが難しいかわかると思います。
宝くじが当たることを夢見るより、確率の問題を解く夢を見るくらい問題解きまくってくださいね。
お疲れさまでした。^^