こんにちは。管理人のMです。
今回は中学数学の確率~コイン~について説明していきます。
と言っても、確率の考え方というのは実は普段の生活の中で自然と使っていると思います。
ジャンケン、宝くじ、ソシャゲのガチャとかは確率の勝負ですよね。
ちなみに僕はギャンブルが強いわけではないですが、一攫千金を夢見てラスベガスとマカオのカジノに行きました。
結果はもちろん惨敗でした。
皆さんもここで確率を極めて大人になったときにラスベガスに行って僕の無念を晴らしてきてください。
この記事のターゲットです。
・学校で確率を習い始めた人
・確率の予習をしたい人
・テスト前に基本だけ押さえたい人
確率の考え方






【確率の考え方】
ある特定の出来事Aが起こる確率pは、次の式で求められる。
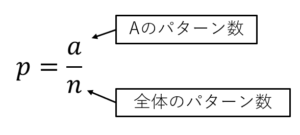
このときAの起こらない確率はqは、次の式で求められる。
![]()
コイン
<例題1>コインを1回投げるとき、表が出る確率を求めよ。


<例題2>コインを3回投げるとき、表が1回・裏が2回出る確率を求めよ。


表を〇、裏を×として図に書き出してみましょう。

このように書き出すと、裏表の出方が全部で8パターンあることが分かります。
全体のパターン数(分母)が分かったので、次は特定のパターン数(分子)を数えます。
今回は表が1回、裏が2回なので、〇が1つで×が2つのパターンですね。

星がついているところが〇が1つで×が2つです。
3パターンあることが分かりますね。
ということで確率は8分の3と求められます。


そして、このように数え上げるときに使う図を『樹形図』と呼んでいます。木の枝分かれみたいですよね。

◎ワンポイント
数えるときには同じパターンをダブって数えてしまったり、パターンが漏れてしまうというミスが多いです。
対策としては書き方にルールを持たせるといいですよ。
今回の例でいえば、各回で〇を上に書いています。こうすれば、パターンの重複や漏れを防ぐことができます。
<例題3>
3枚とも表である確率と少なくとも一枚は裏である確率を求めよ。






まとめ
いかがでしたか?
実はクジ引きやサイコロもまとめて書こうと思ったのですが、量が多くて小分けにすることにしました。
コインの問題は樹形図を正しく書けば必ず正解にたどり着けます。
(コイン100回連続で投げるとか、200枚投げるとかの問題だと樹形図で解くのは現実的ではないですが、それは高校数学でやるので別の機会に説明します。)
余談ですが、日常でコイントスするときに100円玉とか使うと思いますけど、あれは数字が書いてある方が『裏』です。
あまり知られていないので、表と言って100が出ていたらそのまま自分の勝ちにすればいいですし、桜の絵が出たときは「本来はこっちが表だよ」と言えば100%勝てます。
それでは演習編でお待ちしています。
お疲れさまでした。^^