こんにちは。管理人のMです。
今回は中学数学の確率~クジ引き~について説明していきます。
コイン編とクジ引き編をまだ読んでいない方は、そちらから読むことをオススメします。
【中学数学】確率~コイン~【授業編】
【中学数学】確率~クジ引き~【授業編】
サイコロの問題は入試の大好物で頻出の割に点も取りやすい部分だと思います。
しっかり理解していきましょう!
この記事のターゲットです。
・学校で確率を習い始めた人
・確率の予習をしたい人
・テスト前に基本だけ押さえたい人
確率の考え方(復習)
確率の考え方を復習しておきましょう。
確率とは、すべての起こりうるパターンのうちで特定のパターンがいくつあるかを考えるんでしたね。
【確率の考え方】
ある特定の出来事Aが起こる確率pは、次の式で求められる。
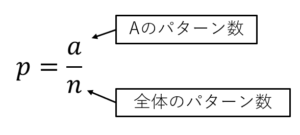
このときAの起こらない確率はqは、次の式で求められる。
![]()
サイコロ
例題1
1から6までの目が出るサイコロを1回振って、奇数が出る確率を求めよ。





例題2
1から6までの目が出るサイコロAとサイコロBを振るとき、出た目の和が4の倍数となる確率を求めよ。






【ポイント】
サイコロを2個振る問題やサイコロを2回振る問題では、表を書いて考える。
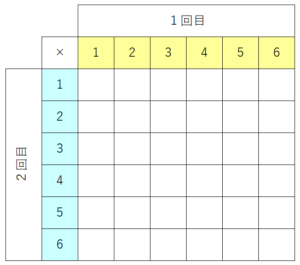
まずは表の骨格を作ります。サイコロは2つとも1から6までの目が出るので、6×6の表を作ります。

今回は2つのサイコロの目の和なので左上に+をつけておくと分かりやすいですね。
そして6×6なので全体のパターン数は36ということが分かりますね。
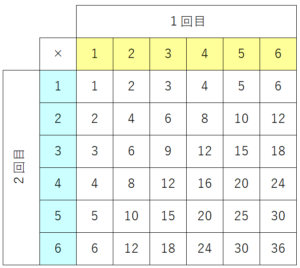
次に表の空いているところに目の和を書いていきます。

小学校の頃の百マス計算を思い出してください。
最後に求められている部分を数えます。
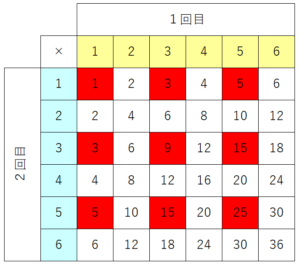
今回は4の倍数なので4,8,12の数を数えます。

4が3つ、8が5つ、12が1つで計9つです。
よって答えは、36分の9となり、約分して4分の1となります。


例題3
1から6までの目が出るサイコロを2回振るとき、出た目の積が奇数となる確率を求めよ。





まとめ
いかがでしたか?
サイコロの問題は表を使って簡単に解けるということが分かったと思います。
表を書くのが面倒に思って頭の中で考えようとする人もいますが、表で考えるのが結局一番早くて正確です。
慣れてきたら頭の中で考えてもいいですが、はじめのうちはしっかりと表に書いて数えることをオススメします。
それでは、演習編でお会いしましょう。
お疲れさまでした。^^