こんにちは。管理人のMです。
当ブログでは初めての高校数学の範囲です。
高校生向けということもあり、ライオンとフクロウの茶番劇を入れるか悩みましたが、入れることにします。
フォーマット変えるのがめんどくさい統一感って大事ですからね。
正直中学生向けでも茶番劇は少し幼い気がしますが、その辺の匙加減はアラサーのおじさんにはよくわからないので見逃してください。
数列って何?






等差数列
-4,-1,2,5,□,11



<例題1>次の数列のx,yに当てはまる数を答えよ。 9,7,5,3,x,y
左から順にみていくと、二つの数の差が-2であることがわかります。
その規則に従うと、x=1,y=-1と求められます。
等差数列では二つの数の差が一定ということをいいましたが、この一定の差を公差といいます。
例題の数列は9から始まり-1で終わりますが、この数列の始まりの数を初項といい、数列の最後の数を末項といいます。

よく公差はd、初項はa1、末項はalと書かれたりしますが、必ずしこう書かなければいけないというわけではないです。
等差数列の一般項



等差数列を数直線上で表現してみましょう。
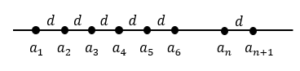
初項a1、公差dとすると
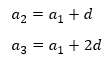
というような式が成り立ちます。
a4=a3+d=a1+3dというように、dを増やしていけば次の数を表現できます。
初項に公差を一つ加えると2項になって、初項に公差を2つ加えると3項になります。
ということは、初項に公差を(n-1)個加えるとn項になりますね。
![]()
これが等差数列の一般項と呼ばれるものです。


an=9+(n-1)(-2)
an=9-2n+2
an=-2n+11
n=79を代入して、a79=-2*79+11=-147かな?


等差中項
<例題2> 3,x,11がこの順に等差数列をなすとき、xの値を求めよ。
等差数列なので、公差をdとすると、
x-3=dと書けますし、
11-x=dとも書けますね。
これを連立方程式として解けばxが求められそうです。
右辺がどちらもdなので、
x-3=11-x
2x=14
x=7と求められました。
さて、この7という答えに注目してほしいんですが、これは3と11の平均と同じ値ですね。
このように等差数列の真ん中の数は前後の数の平均になります。
この真ん中の数のことを等差中項といいます。
まとめ
今回は規則を見つけたり、一般項を求めたり、等差中項の性質を使ったりして等差数列の値を求めるということをやりました。
演習問題を用意していますので、演習編でお会いしましょう!


