こんにちは。管理人のMです。
等比数列①の演習編です。授業編を読んでいない方はぜひ授業編を読んできてください。
演習問題
問1. 次の等比数列の一般項と第4項を求めよ。
(1) 初項5、公比2/3
(2) 初項-3、公比3
(3) 初項1/2、公比-1/2
問2. 第3項が12、第6項が-96となる等比数列の初項と公比を求めよ。
問3. -27, x, -3がこの順で等比数列となるとき、xの値を求めよ。
問1 解答と解説
(1)解答例です。

与えられた初項と公比を代入すれば一般項が求められます。
一般項が求められたら、nの値を代入して計算するだけです。
(2)解答例です。

これも与えられた初項と公比を代入することで一般項が求められます。
一般項の答え方ですが、まとめられる部分はできるだけまとめるクセをつけましょう。
今回でいえば、
![]()
という単に代入した形で終えるのではなく、初項の3を公比に組み込むとより整理された式になります。
n-1乗にさらに一つ追加されるのでn乗になりますね。
一般項が求められたら、あとはnの値を代入して計算するだけです。
(3)解答例です。

これも与えられた初項と公比を代入することで一般項が求められます。
(2)と同じく、まとめられる部分はできるだけまとめてくださいね。
今回は、初項が1/2で公比が(-1/2)となっています。
なんとなくまとめられそうですが、そのままではまとめられないので、少し工夫しましょう。
初項の1/2をなんとかして公比の-1/2で表現することを考えます。
青の波線で書かれている部分に注目してほしいのですが、
![]()
このように変形すると、公比の-1/2が一つ増えてn乗にできます。
このようにパッと見で初項と公比が異なる値であっても、少し工夫するだけでまとめられることがあるので、
代入して一般項を求めたら、本当にまとめられる部分はないか?を探すようにしてください。
問2 解答と解説
解答例です。
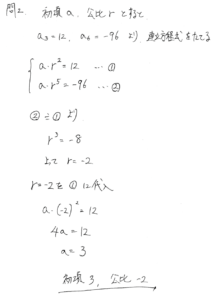
<解答の方針>
初項をa、公比をrとおいて連立方程式を立てる。
第3項と第6項について方程式を2本作れるので、それらの連立方程式を解いていくと初項と公比が求められます。
問3 解答と解説
解答例です。

<解答の方針>
等比中項の考え方を用いる。
⇒真ん中の数の2乗=前後の数の積
等比中項の関係式「真ん中の数の2乗=前後の数の積」より計算していきましょう。
xが正と負で2つ出てきますが、どちらも答えです。
実際にそれぞれの値の場合には次のような数列になります。

xがどちらの値であっても等比数列が成立することがわかりますね。
以上で等比数列①演習編は終わりです。
お疲れさまでした。^^