等比数列の和【授業編】

こんにちは。管理人のMです。
今回は『等比数列の和』の公式について説明していきます。

公式というと「暗記だー！！」となってしまう人も多いですが、等比数列の和の公式は暗記する必要はありません。
複雑な公式に見えて実は簡単に求められるので、求め方をしっかりと理解しましょう。

等比数列の和の例題

例題をみてみましょう。

初項1、公比-3の等比数列だね。一般項は求められそう！

和を求めろと言っていますね。足し算してみるとどうでしょうか？

1+(-3)+9+(-27)+81+(-243)＋・・・

増えたり減ったりしていって全然計算できないよ。。。

数字をひたすら足していくだけでは出ませんよ。

やらすなよ！！

公式のありがたみや便利さを知ってほしいので一度やってもらいました。

等比数列の和の公式をいうものがあるので、それを紹介します。

等比数列の和の公式

公式カモン！！

上機嫌ですね。等比数列の和の公式はこちらです。

え、やばくない？こんなの覚えられないよ。。

安心してください。むやみに覚える必要はありません。ちゃんと自力で求めることができますよ。

公式を暗記しようと何度も何度も公式を書き続けている人はいませんか？

むりやり覚えた公式はすぐに忘れたり使い方を間違えたりしやすいです。公式を自分で導けるということが数学の勉強ではとても重要になってきます。

誰に話してるの！！はやく説明して！！！

等比数列の和の公式の導出

数字をひたすら足していくだけでは求められないと言いましたが、文字で考えてみてはどうでしょうか？

文字かー。初項をaとして公比をrとして初項から第n項までの足し算をすると・・・

和をSnとおいて、初項から第n項（一般項）までの和は次のようになります。

次に和Snをr倍したものを考えます。（r倍する理由はすぐにわかります。）

見比べてみると色枠で囲まれた部分が同じであることがわかりますね。

同じなので引き算をすると消すことができます。

1-r≠0のとき、両辺を1-rで割ると

冒頭でr<1のとき、r>1のときと分けて公式を書いていましたが、実は分ける必要はありません。
r<1のときは分母も分子も正ですが、r>1のときは分母も分子も負になります。
それを正にするために引き算の順序を逆転させているだけですが、そんなことをしなくても分母も分子もマイナスなら符号を打ち消しあうのであまり考えなくて大丈夫です。

ここで一つ注目してほしいのが、1-r≠0のときという部分です。
数学のルールで0で割ることはできないので「0ではないよ」と示すことは必要であり、
この公式はr≠1のときにしか使えないということを意味しています。

では、r=1だったらどうなるのでしょう？

分母が0になってはいけないので別の考え方が必要そうですね。

そもそもr=1ということは公比が1なので、どのような数列
になるかというと

r=1なのでaをひたすら足していくということです。
aがいくつあるかというと、上の図の通りn個なので、

となります。

例題の解答

おーー、等比数列の和の公式が分かったよ！

例題の解答です。

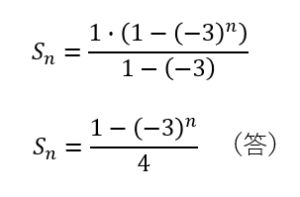
まとめ

いかがでしたか？

一見難しそうに見える公式も成り立ちをしっかりと理解すれば、自分で導けるということが分かってもらえたかと思います。

公式を覚えること自体を否定するつもりはありませんが、成り立ちを知って自分で求められることが重要です。
公式の暗記は問題を解いていく中で自然に覚えてしまうというのが理想形です。

公式を自然に覚えてしまうために演習編で問題をガンガン解いていきましょう。
それでは演習編でお会いしましょう！

お疲れさまでした。＾＾