こんにちは。管理人のMです。
三平方の定理の演習編です。授業編を読んでいない方はぜひ授業編を読むことをオススメします。
演習問題
<問1>次のxとyとzを求めよ。

<問2>次のうち、直角三角形であるものをすべて選べ。
(ア)辺がそれぞれ6cm,10cm,8cmの三角形
(イ)辺がそれぞれ4cm,8cm,2cmの三角形
(ウ)辺がそれぞれ15cm,8cm,17cmの三角形
<問3>次の直角三角形の斜辺の長さを求めよ。

問1 解答と解説
<問1(1)>
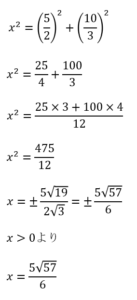
まずは三平方の定理を使ってxの2乗を求めます。
xの2乗からxにするときには±を忘れずに!
分母に√がつく場合は有理化が必要で、有理化は分母の√と同じものを分母と分子にかけるんでしたね。
今回は√3をかけてあげると有理化できます。
そしてxは三角形の辺の長さなので正の値が答えになります。
どうでしょうか?
少し値が大きくて計算のしづらさがあったかもしれませんが、これができれば計算力はバッチリです。
<問2(2)>
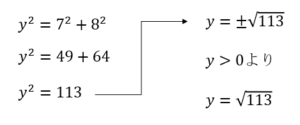
これも同じですね。
√の中身が大きいので、外に出せる数があるかも?と思ったかもしれませんが、113は素数なので√がついたままで答えになります。
<問3(3)>
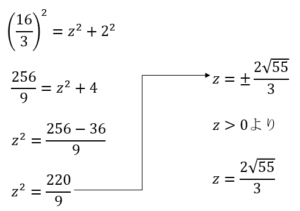
(1)と(2)は求めたい値が斜辺でしたが、今回は斜辺ではありません。
でもやることは同じく三平方の定理に代入してガリガリ計算していきましょう。
移項するときの符号に注意が必要です。
問2 解答と解説
答えは(ア)と(ウ)です。
直角三角形かどうかは三平方の定理が成り立つかどうかを調べればよかったですね。
このときに注意するのは、直角三角形は斜辺が一番長いので一番大きい値を斜辺の部分に代入して計算しましょう。
今回の問題では、すべて整数になっていますよね。
実は、整数比になる直角三角形というのはそこまで多くありません。
入試で扱う範囲であれば、3つ覚えておけば十分で、それを覚えていれば計算せずとも答えにたどり着けました。
覚えるべき直角三角形は演習3で扱っています。
問3 解答と解説
(1)(2)(3)は三平方の定理を使ってガリガリ計算して求めることができますが、覚えていれば計算無しで一発で解けるので、ここに出てきた三角形はすべて覚えてしまいましょう。
(4)(5)は有名角の直角三角形なのでこちらも絶対に覚えてください。
<問3(1)~(5)>
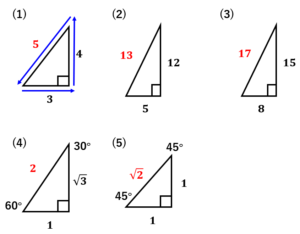
赤字が答えです。
全部覚えてしまいましょう。
覚え方ですが、これは念仏のように唱え続けるのが一番です。
直角は右下に固定して、左下から青矢印の順に唱えていきましょう。
3:4:5
5:12:13
8:15:17
1:√3:2
1:1:√2
どうですか?全部唱えても10秒くらいだと思います。
これを一日3分くらい唱え続けてください。
覚えているだけでかなり役立つのでここは頑張ってくださいね。
以上で三平方の定理の演習編は終わりです。
お疲れさまでした。^^