こんにちは。管理人のMです。
中学数学 確率の演習編です。
授業編を読んでいない方は授業編を読むことをオススメします。
まずはざっくりと確率の復習をしておきましょう。
確率の考え方
確率とはすべての起こりうるパターンのうちで特定のパターンがいくつあるかということを考えることです。
よって、特定のAが起こる確率pは次式で求められます。
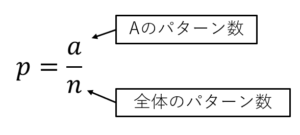
また、Aが起こらない確率qは次式で求められます。
![]()
復習はこのくらいにして、問題演習に進みましょう。
演習問題
問1 3枚のコインを同時に投げるとき、次の確率を求めよ。
(1)3枚とも表の確率
(2)1枚が表で2枚が裏の確率
(3)少なくとも1枚は裏の確率
問2 アタリが3本、ハズレが1本入っているクジについて、次の確率を求めよ。
(1)このクジを2回引いたときに2本とも当たる確率(ただし、引いたクジは元に戻す)
(2)このクジを2回引いたときに2本とも当たる確率(ただし、引いたクジは元に戻さない)
(3)このクジを2回引いたときに少なくとも1本は当たる確率(ただし、引いたクジは元に戻す)
(4)このクジを2回引いたときに少なくとも1本は当たる確率(ただし、引いたクジは元に戻す)
問3 1から6までの目が出るサイコロAとサイコロBを振るとき、次の確率を求めよ。
(1)Aの目とBの目の和が7以上となる確率
(2)Aの目からBの目を引いた差が負になる確率
(3)Aの目とBの目の積が10以上20以下となる確率
問1 (コイン)解答と解説
3枚のコインを同時に投げるという問題です。


ポイント
コインを3回投げるとき、1回目が表が出たからといって、2回目3回目に表が出にくくなることはありません。
同じようにコインを3枚同時に投げて1枚が表が出たからといって、残りの2枚で表がが出にくくなることはありません。
1回のコイントスで表が出る確率は常に2分の1です。
<問1-(1)>
ということで、同じように考えていきましょう。
樹形図で全パターン書き出して、当てはまるパターンを数えるという王道で最強の手法を使いましょう。
表が〇、裏が×で樹形図を作ります。
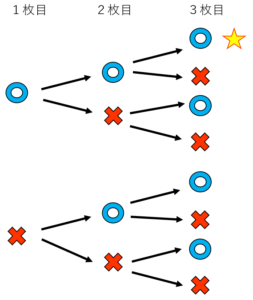
3枚とも表なのは、〇⇒〇⇒〇となる1パターンだけですね。
一方で全体では何パターンあるかというと、樹形図から8パターンあることが分かります。
よって求める答えは、8分の1です。
<問1-(2)>
面倒くさがらずに樹形図を書いて数える。これが大事です。
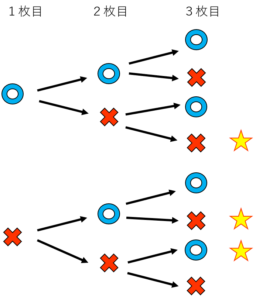
1枚が〇で2枚が×となっているのは3パターンありますね。
全体は8パターンなので、求める答えは、8分の3です。
<問1-(3)>
少なくとも1枚は裏が出るということは、裏が0枚ではないということです。
「裏が0枚」とは「3枚とも表」と同じですね。
全体から3枚とも表のパターンを除いたものが答えです。
(1)で3枚とも表は1パターンあることが分かっています。よって少なくとも1枚が裏のパターンは7つあることが分かります。
よって、求める答えは8分の7です。
「さっきまで散々面倒くさがらずに樹形図を書けと言ってたくせに樹形図書いてないじゃん」と思った方、
当然樹形図を書いて数えても答えは出ます。
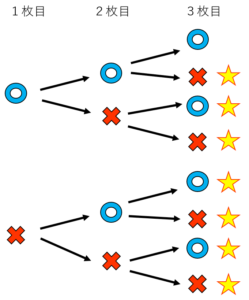
確率で王道にして最強の解き方は樹形図です。
ですが、楽に解ける方法を知っておくのも損はしませんよ。
問2 (クジ引き)解答と解説
クジ引きの問題です。
よく似た問題ですが、一度引いたクジを戻すか戻さないかというところに違いがあります。
アタリが3本・ハズレが1本の合計4本のクジで引いたクジを戻すときは、同じものを連続して引くことがあり得ますが、
引いたクジを戻さないときは、同じものを連続して引くことは無いですよね。
なので、アタリに1~3、ハズレに4の番号をつけて考えてみましょう。
<問2-(1)>
引いたクジを戻すので、1⇒1や2⇒2と引くこともあり得ます。
樹形図を書くとこんな感じです。
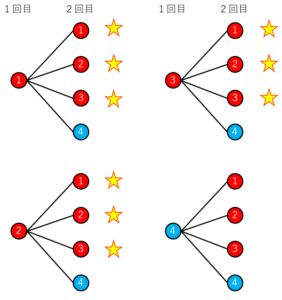
2回とも当たっているのは☆のパターンなので、9パターンあります。
全体では16パターンあるので、求める確率は16分の9となります。
<問2-(2)>
引いたクジを戻さないので、さっきの問題のように1⇒1や2⇒2と引くこともありません。
樹形図はこんな感じです。
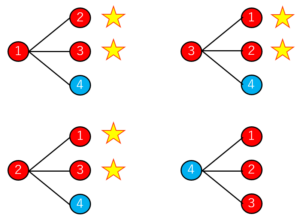
2回とも当たっているのは☆のパターンなので、6パターンあります。
全体では12パターンあるので、求める確率は12分の6で約分して2分の1です。
<問2-(3)>
「少なくとも1つ」という場合は、全部数えてもいいんですけど、楽に解く方法がありましたね。
「一つも当たらない=2つともハズレ」の確率を求めて1から引けば求められます。
今回は少なくとも1つアタリなので、アタリが一つもない確率を求めて、それを1から引けばよさそうです。
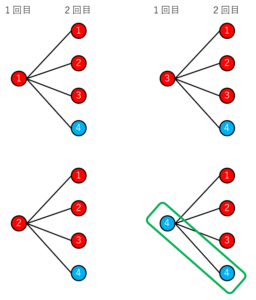
一つもアタリがないのは、樹形図の緑色で囲われた部分の1パターンだけです。
この確率は16分の1なので、求める確率は
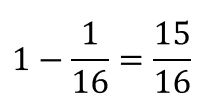
となります。
<問2-(4)>
クジ引き最後の問題です。
これも少なくとも1本当たる確率なので、同じ考え方が使えそうです。
ただし、引いたクジは戻さないので樹形図は(2)の形です。
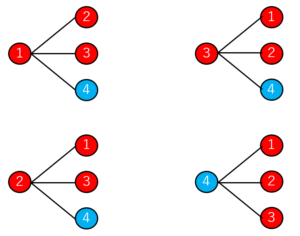
・・・・・。
アタリが一つもないパターンがないですね。
なので求める答えは1です。
少し意地悪な問題でした。
問3 (サイコロ)解答と解説
サイコロの問題は表を書いて100マス計算の要領で表を埋めることがスタートです。
<問3-(1)>
表を作って数えます。
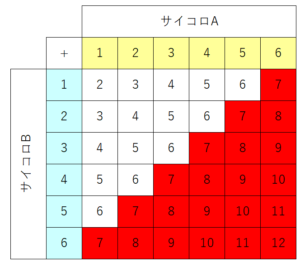
目の和が7以上になっているのは赤マスの部分で、21個あります。
よって、求める答えは36分の21、約分して12分の7です。
<問3-(2)>
表を作って数えます。
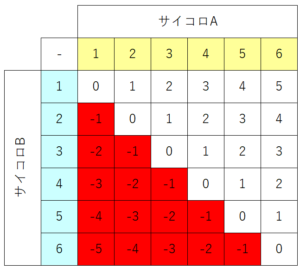
Aの目-Bの目が負になるのは赤マスの部分で、15個あります。
よって、求める答えは36分の15、約分して12分の5です。
<問3-(3)>
表を作って数えます。
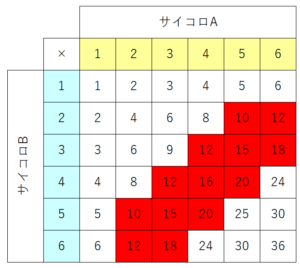
目の積が10以上20以下となっているのは赤マスの部分で13個あります。
よって、求める答えは36分の13です。
以上で、確率の演習編は終了です。
樹形図書いたり表を書いたり大変でしたね。
高校数学ではもう少し楽に解けたりもするんですけど、樹形図や表を書いて考える(=数える)ということが確率の基本であることを忘れずにどんどん問題解いていってください。
お疲れ様でした。^^